Caros leitores, o problema do pêndulo cônico é aqui construído segundo os comandos básicos do aplicativo gnuplot. Os objetos presentes (circle, arrow e label) na animação são implementados facilmente.
Aplicações da Linguagem de programação C/C++, e de software livre, tipo: gnuplot, scilab, lazarus e outros, em problemas da Física e da Matemática.
segunda-feira, 14 de dezembro de 2015
Animação com gnuplot: Pêndulo Cônico
Pêndulo Cônico
Caros leitores, o problema do pêndulo cônico é aqui construído segundo os comandos básicos do aplicativo gnuplot. Os objetos presentes (circle, arrow e label) na animação são implementados facilmente.
Caros leitores, o problema do pêndulo cônico é aqui construído segundo os comandos básicos do aplicativo gnuplot. Os objetos presentes (circle, arrow e label) na animação são implementados facilmente.
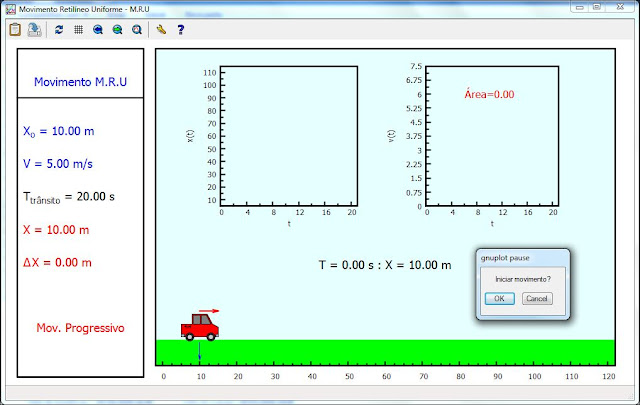
Animação com gnuplot: Movimento Uniforme
MOVIMENTO RETILÍNEO UNIFORME (M.R.U)
Caros leitores, uma ilustração simples do movimento retilíneo uniforme e os correspondentes gráficos do M.R.U. é aqui construído segundo os comandos básicos do aplicativo gnuplot. Os objetos presentes na animação (polygon, circle, arrow, e label) são implementados facilmente. As equações físicas utilizadas são as equações trabalhadas nas aulas de Física.
Caros leitores, uma ilustração simples do movimento retilíneo uniforme e os correspondentes gráficos do M.R.U. é aqui construído segundo os comandos básicos do aplicativo gnuplot. Os objetos presentes na animação (polygon, circle, arrow, e label) são implementados facilmente. As equações físicas utilizadas são as equações trabalhadas nas aulas de Física.
sábado, 25 de abril de 2015
Sistemas de Equações Diferenciais Ordinárias: Métodos de Runge-Kutta de Ordem p
1.0 Introdução
Em duas postagens anteriores, apresentamos os métodos numéricos de Runge-Kutta com o intuito de resolver equações diferenciais de primeira ordem, mais especificamente em problemas de valor inicial (P.V.I) de primeira ordem. Entretanto, a maioria das equações diferenciais com importância prática, são de ordem maior que $1$ ou então são sistemas de equações diferenciais. Nesta postagem, nosso intuito é o de apresentar o procedimento de como resolver um sistema de equações diferenciais de primeira ordem e, também, o de resolver numericamente uma equação diferencial de ordem elevada, usando os métodos de Runge-Kutta.
1.1 - Sistemas de Equações Diferenciais Ordinárias
Consideremos um sistema de $n$ equações diferenciais de primeira ordem:
\begin{equation}
\begin{array}{llll}
y'_1=f_{1}(x, y_1, y_2, \cdots, y_n)\\
y'_2=f_{2}(x, y_1, y_2, \cdots, y_n)\\
\vdots\\
y'_n=f_{n}(x, y_1, y_2, \cdots, y_n)
\end{array}
\end{equation}
o qual pode ser escrito, como: $$\mathbf{y' = f(x, y)} , $$ onde $\mathbf{y}$, $\mathbf{y'}$ e $\mathbf{f}$ são vetores com componentes $\mathbf{y_i}$, $\mathbf{y'_i}$ e $\mathbf{f_{i}(i=1, 2, \cdots, n)}$, respectivamente. Para que esse sistema possua uma única solução é necessário impormos uma condição adicional sobre $\mathbf{y}$. Esta condição é usualmente da forma: $$\mathbf{y(x_{0}) = y_{0}} , $$ para um dado número $\mathbf{x_0}$ e um vetor $\mathbf{y_0}$
Agora descreveremos como os métodos apresentados nas postagens anteriores para a solução de equações diferenciais de primeira ordem podem ser aplicados para resolver sistemas de equações diferenciais de $1^a$ ordem. Para efeito de simplicidade, e sem perda de generalidade, consideramos apenas o caso em que $n=2$, isto é, o sistema possui apenas duas equações, e para maior clareza usaremos a notação:
\begin{equation} \left\{
\begin{array}{llll}
y' = f(x, y, z)\\
z' = g(x, y, z)\\
y(x_{0})=y_{0}\\
z(x_{0})=z_{0} \ \ \ x \in \left[x_{0}, b \right]
\end{array}
\right.
\end{equation}
Assim, se desejamos resolver o sistema $(2)$ pelo método de Euler (Runge-Kutta de ordem 1), teremos:
\begin{equation}
\begin{array}{ll}
y_{i+1}=y_i + hf(x_i, y_i, z_i)\\
z_{i+1}=z_i + hg(x_i, y_i, z_i)\\
\end{array}
\end{equation}
que será aplicado passo a passo.
No caso de escolhermos o método de Runge-Kutta de $4^a$ ordem para resolvermos o sistema $(2)$, teremos as seguintes expressões:
\begin{equation}
\begin{array}{ll}
y_{i+1}=y_i + \frac{h}{6}(k_1 + 2k_2 + 2k_3 +k_4)\\
z_{i+1}=z_i + \frac{h}{6}(l_1 + 2l_2 + 2l_3 + l_4)\\
\end{array}
\end{equation}
onde
- $k_1 = f(x_i, y_i, z_i)$
- $l_1 = g(x_i, y_i, z_i)$
- $k_2 = f(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2}k_{1}, z_i + \frac{h}{2}l_1)$
- $l_2 = g(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2}k_{1}, z_i + \frac{h}{2}l_1)$
- $k_3 = f(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2}k_{2}, z_i + \frac{h}{2}l_2)$
- $l_3 = g(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2}k_{2}, z_i + \frac{h}{2}l_2)$
- $k_4 = f(x_{i}+h, y_{i} + hk_{3}, z_i + l_3)$
- $l_4 = g(x_{i}+h, y_{i} + hk_{3}, z_i + l_3)$
Nota: A aplicação de um método numérico a um sistema de equações ordinárias de primeira ordem se processa como no caso de uma única equação, só que aqui devemos aplicar o método numérico a cada uma das componentes do vetor.
Finalmente, mostraremos como equações de ordem superiores a 1 podem ser escritas e portanto resolvidas como um sistema de equações de primeira ordem. Consideremos a equação diferencial de ordem $n$: $$y^{(n)} = f(x, y, y', \cdots, y^{(n-1)}).$$
com as condições iniciais: $$y(x_0) = y_0, \ \ \ y'(x_0) = y'_0, \ \ \cdots, \ \ y^{(n-1)}(x_0)=y^{(n-1)}_0.$$
Novamente, para simplicidade, mas sem perda de generalidade, consideremos a equação diferencial de segunda ordem:
\begin{equation} \left\{
\begin{array}{lll}
\frac{d^2\,y}{dx^2}+q(x)\frac{dy}{dx} = r(x,y)\\
y(x_{0})=y_{0}\\
\frac{d\,y}{dx}|_{x_0}=y'_{0}
\end{array}
\right.
\end{equation}
Podemos resolver qualquer equação diferencial de ordem elevada reduzindo-a a um sistema de equações diferenciais de primeira ordem. Para tanto basta fazer uma mudança adequada de variável, para a equação de segunda ordem, (5). Fazendo a seguinte mudança de variável: $$z(x, y) = \frac{d\,y}{dx}, $$
a equação (5) é escrita como um conjunto de duas equações diferenciais de $1^a$ ordem, ou seja, o P.V.I, definido por (5), se reduz a:\begin{equation}
\left\{
\begin{array}{llll}
\frac{d\,y}{dx} = z(x, y)\\
\frac{d\,z}{dx}= r(x, y) - q(x)z(x, y)\\
y(x_{0})=y_{0}\\
z(x_{0})=z_{0}
\end{array}
\right.
\end{equation}
Observe que o conjunto de equações em (6) pode ser escrito na forma:
\begin{equation} \left\{
\begin{array}{llll}
y' = f(x, y, z)\\
z' = g(x, y, z)\\
y(x_{0})=y_{0}\\
z(x_{0})=z_{0}
\end{array}
\right.
\end{equation}
Nota: Ao reduzir o P.V.I. definido pela equação $(5)$, a um sistema de E.D.O. de primeira ordem, o problema passa a ser análogo ao P.V.I definido pelo sistema (2).
Portanto, para a solução da equação diferencial ordinária de $2^a$ ordem $(5)$, é necessário que as equações diferenciais ordinárias de $1^a$ ordem, apresentadas em $(7)$ sejam resolvidas. A seguir, apresenta-se a solução destas equações, usando o método de Euler e o Método de Runge-Kutta de $4^a$ ordem.
1.3 - Exemplo usando o Método de Euler e o de Runge-Kutta de $4^a$ Ordem
A equação diferencial ordinária de $2^{a}$ ordem escolhida será:
\begin{equation}
\frac{d^{2}y}{dx^{2}}-y=e^{x}
\end{equation}
com $x$ variando de $0$ a $1$, com as seguintes condições iniciais:
\begin{equation}
\left\{
\begin{array}{ll}
y(0)=1\\
\frac{dy}{dx}|_{x_0}=0
\end{array}
\right.
\end{equation}
Primeiro passo: é reduzir esta equação diferencial de $2^a$ ordem para um conjunto de $2$ equações diferenciais ordinárias de $1^a$ ordem:
\begin{equation}\left\{
\begin{array}{ll}
\frac{dy}{dx} = z \\
\frac{dz}{dx} =y+e^{x}
\end{array}
\right.
\end{equation}
De acordo com as condições iniciais em $(9)$, tem-se $x_0 = 0$ e $y_0 = 1$.
A solução da equação diferencial ordinária de $2^a$ ordem, $(8)$, com a condição inicial $(9)$ é:
\begin{equation}y(x)=\frac{1}{4}[e^{x}(1+2x)+3e^{-x}].
\end{equation}
A
solução numérica é encontrada com a avaliação das equações do Método de
Euler (Runge-Kutta de $1^a$ ordem), e do Método de Runge-Kutta de $4^a$ ordem, apresentadas respectivamente pelas equações (3) e (4), com
a condição inicial, $x_0=0$ e $y_0=0$.
Nota: vale lembrar que, a solução aproximada da equação diferencial de segunda ordem encontra-se na primeira componente do vetor, isto é, apenas nos interessa o valor de $y_i$, apesar de termos de calcular, a cada passo, todas as componentes do vetor.
Para efeitos de comparação, usaremos três valores para o passo h=0.1 (Figura 1), h=0.01 (Figura 2) e h=0.001 (Figura 3), juntamente com a solução algébrica (8).
1.3.1 - Resultados obtidos pelos Métodos de Euler e de Runge-Kutta de $4^a$ ordem
 |
| Figura 1: Solução da E.D.O. de $2^a$ ordem com passo $h=0.1$ |
 |
| Figura 2: Solução da E.D.O. de $2^a$ ordem com passo $h=0.01$ |
 |
| Figura 3: Solução da E.D.O. de $2^a$ ordem com passo $h=0.001$ |
1.4 - Métodos de Runge-Kutta implementado em linguagem de programação.
Um programa escrito em C/C++ é apresentado a seguir. Uma parte do código-fonte pode ser retirada sem problemas, pois trata-se de rotinas voltadas para mostrar a interatividade entre o aplicativo gnuplot (para plotar gráficos) e a linguagem programação C/C++. Os dados obtidos são impressos em um arquivo de nome "runge_kutta.txt", podendo ser plotado usando o Origin, qtiplot, MatLab, SciLab, dentre outros.
/*========================*/
/* Métodos de Runge-Kutta - E.D.O. de 2ª ordem */
/*=============================*/
#include <stdio.h>
#include <stdlib.h>
#include <cmath>
FILE *fp;
static char nome[]="runge_kutta.txt";
void scrip_gnuplot(char str[25])
{
fp=fopen("rk4_2_ordem.plt", "w");
fprintf(fp, "reset\n");
fprintf(fp, "set title \"Métodos de Runge Kutta\" \n");
fprintf(fp, "set xlabel \"Xn\" \n");
fprintf(fp, "set ylabel \"Yn\" \n");
fprintf(fp, "set key bottom \n" );
fprintf(fp, "set term jpeg \n" );
fprintf(fp, "set output \"Runge_Kutta.jpg\" \n");
fprintf(fp, "plot \'%s\' u 1:2 t \" Euler \" w lp ls 7 lc 1 lw 1, \'%s\' u 1:3 t \" Runge-Kutta 4a ordem \" w lp ls 7 lc 2 lw 1\n", str, str);
fprintf(fp, "replot \'%s\' u 1:4 t \" Analitica \" w l lc -1\n", str);
fprintf(fp, "set output; set term wxt \n");
fprintf(fp, "replot \n");
fprintf(fp, "pause -1 \"Continuar?\" ");
fclose(fp);
}
double f(double x, double y, double z)
{
return z; // equação diferencial: dy/dx=f(x,y,z)
}
double g(double x, double y, double z)
{
return (y+exp(x)); // equação diferencial: dz/dx=g(x,y,z)
}
double y(double x) // solução analitica da equação diferencial
{
return (0.25*(exp(x)*(1.0+2.0*x)+3.0*exp(-x)));
}
double euler(double x, double y, double *z, double h)
{
y = y + h*f(x,y,*z); // método de euler
*z = *z + h*g(x,y,*z);
return y;
}
double runge_kutta_4(double x, double y, double *z, double h)
{
double k1, k2, k3, k4, l1, l2, l3, l4;
k1 = h*f(x, y, *z); // método de runge-kutta de ordem 4
l1 = h*g(x, y, *z);
k2 = h*f(x+0.5*h, y+0.5*k1, *z+0.5*l1);
l2 = h*g(x+0.5*h, y+0.5*k1, *z+0.5*l1);
k3 = h*f(x+0.5*h, y+0.5*k2, *z+0.5*l2);
l3 = h*g(x+0.5*h, y+0.5*k2, *z+0.5*l2);
k4 = h*f(x+h, y+k3, *z+l3);
l4 = h*g(x+h, y+k3, *z+l3);
y = y + (k1+2*k2+2*k3+k4)/6.0;
*z = *z + (l1+2*l2+2*l3+l4)/6.0;
return y;
}
int main(void)
{
double x0, y0, z0, xmax, h; // variaveis de entrada
double xn, yn_e, yn_rk4, *zn_e, *zn_rk4; // variaveis incrementadas
double z0_e, z0_rk4;
// Dados de entrada:
x0=0.0;
y0=1.0;
z0=0.0;
xmax=1.0;
h=0.01;
// -----------------
fp=fopen(nome,"w");
xn = x0;
yn_e = yn_rk4 = y0;
z0_e = z0_rk4 = z0;
zn_e = &z0_e;
zn_rk4 = &z0_rk4;
while (xn<xmax)
{
fprintf(fp, "%f \t %f \t %f \t %f\n", xn, yn_e, yn_rk4, y(xn));
yn_e = euler(xn, yn_e, zn_e, h);
yn_rk4 = runge_kutta_4(xn, yn_rk4, zn_rk4, h);
xn = xn+h;
}
fclose(fp);
scrip_gnuplot(nome);
system("gnuplot rk4_2_ordem.plt");
return 0;
}
1.5 - Conclusão
A
resolução numérica pode ter grau crescente de aproximação, de acordo
com o método numérico escolhido e da escolha do valor do passo de
integração. Comparando os resultados da solução numérica usando o método de Euler com os resultados da solução usando o método de Runge-Kutta de $4^a$ ordem, observa-se que neste segundo método a precisão é sempre maior, mesmo com o uso de um passo $10$ vezes maior.
Assim,
diante dos exemplos estudados, concluímos que o Método de Runge-Kutta
de $4^a$ ordem é bastante eficaz para resolução de sistemas de EDOs de primeira ordem, o que explica o porquê de ser o método de passo simples mais
utilizado por engenheiros e cientistas na resolução numérica de equações
diferenciais ordinárias.
1.6 - Referências
[1]
W. E. Boyce, C. R. Diprima, "Equações Diferenciais Elementares e
Problemas de Valor de Contorno", LTC, Rio de Janeiro, 2011.
[2] M. A. G. Ruggiero, V. L. R. Lopes, "Cálculo Numérico: Aspectos Teóricos Computacionais", Makron Books, São Paulo, 1996.
[3] G. Baratto, "Solução de Equações Diferenciais Ordinárias Usando Métodos
Numéricos", Departamento de Eletrônica e Computação - Estudo de Casos em
Engenharia Elétrica - UFSM, 2007.
[4] L. N. de Andrade, "Cálculo Numérico: Introdução à Matemática Computacional", Departamento de Matemática - UFPB, 2013.
[4] L. N. de Andrade, "Cálculo Numérico: Introdução à Matemática Computacional", Departamento de Matemática - UFPB, 2013.
sexta-feira, 24 de abril de 2015
Solução Numérica de Equações Diferenciais Ordinárias usando o Método de Runge-Kutta
1.0 INTRODUÇÃO
A resolução de equações diferenciais é um problema importantíssimo porque possui aplicações a diversas áreas do conhecimento tais como Matemática Aplicada, Física, Engenharia, Biologia, Economia e Computação Gráfica.
Devido à impossibilidade de se determinar a solução exata na maioria dos casos, desenvolveram-se técnicas de determinação de solução numérica aproximadas da equação.
Aqui, iremos nos concentrar em problemas de valor inicial
(P.V.I.) em sua forma mais simples que são as equações diferenciais
ordinárias de primeira ordem:
\begin{equation} \left\{
\begin{array}{ll}
\frac{dy}{dx}=f(x,y)\\
y(x_0)=y_0
\end{array}
\right.
\end{equation}
Uma solução exata de um P.V.I. do tipo (1) é uma função derivável cujo gráfico passa pelo ponto $(x_0, y_0)$. Uma solução aproximada é uma tabela de valores que inicia com $(x_0, y_0)$, próximos do gráfico da função que seria a solução da equação.
Nesta postagem, nosso intuito é o de apresentar as idéias básicas e as principais propriedades dos métodos de Runge-Kutta. Uma demonstração breve do método de Runge-Kutta de $2^a$ ordem é apresentada. E, em seguida, apresentamos as regras de implementação dos métodos de Runge-Kutta de $3^a$ e $4^a$ ordem, concluindo com exemplos práticos de sua aplicação.
1.1 - OS MÉTODOS DE RUNGE-KUTTA
Os métodos de Runge-Kutta são uma família de métodos
iterativos para aproximar numericamente a solução de uma equação
diferencial ordinária. Os matemáticos alemães Carl David Runge (1856-1927)
e Martin Wilhelm Kutta (1867-1944), construíram os métodos de tal modo que sejam
equivalentes a aproximar a solução exata de uma equação diferencial
pelos primeiros $n$ termos de uma expansão em série de Taylor.
As características de eficiência e simplicidade de implementação, conferem aos métodos de Runge-Kutta grande popularidade, sendo um dos mais utilizados por engenheiros e cientistas.
1.1.1 - Propriedades dos Métodos de Runge-Kutta
A idéia básica destes métodos é aproveitar as qualidades dos métodos de série de Taylor (ordem elevada) e ao mesmo tempo eliminar sua maior dificuldade que é o cálculo de derivadas de $f(x,y)$ que torna os métodos de série de Taylor computacionalmente inaceitáveis.
Características dos métodos de Runge-Kutta de ordem $p$:
- são de passo simples (auto-iniciantes);
- não exigem o cálculo de derivadas parciais de $f(x,y)$;
- necessitam apenas do cálculo de $f(x,y)$ em determinados pontos do intervalo $[x_{i}, x_{i+1}]$ (os quais dependem da ordem dos métodos);
- expandindo-se $f(x,y)$ por Taylor em torno de $(x_i , y_i)$ e agrupando-se os termos em relação às potências de $h$, a expressão do método de Runge-Kutta coincide com a do método de Taylor de mesma ordem.
Na postagem "Solução Numérica de Equações Diferenciais Ordinárias usando o Método de Euler", vimos que o método de Euler para resolução do P.V.I, $y'=f(x,y)$, $y(x_0)=y_0$, consiste na aplicação das fórmulas:
\begin{equation}
x_{i+1}=x_i+h
\end{equation} e \begin{equation}
y_{i+1}=y_i+k_1, \ \ \mbox{para} \ \ i=0, 1, 2, \cdots,
\end{equation}
onde $k_1=hf(x_i, y_i)$ e $h$ chamado passo ou incremento de integração é próximo de $0$.
O método de Runge-Kutta é um aperfeiçoamento do método de Euler e consiste em somar ao $y_i$ não apenas um valor de $k_1$, mas uma média de vários valores de $k_1, \,k_2, \,k_3, \cdots $.
1.1.2 - Síntese do Método de Runge-Kutta de Ordem $p$
- Fórmula geral do Método de Runge-Kutta: $$y_{i+1}=y_i + h \phi(x_i, y_i; h)$$,
- $\phi(x_i, y_i; h)$ é chamada função incremento, e pode ser interpretada como a inclinação no intervalo considerado.
- Fórmula geral da função incremento de ordem $p$: $$\phi(x, y; h)=b_1k_1+b_2k_2+ \cdots + b_pk_p , $$
- $k_1=f(x, y)$
- $k_2=f(x+c_2h, y+ha_{21}k_1)$,
- $k_3=f(x+c_3h, y+h(a_{31}k_1+a_{32}k_2))$,
- $\cdots$
- $k_p=f(x+c_ph, y+h(a_{p1}k_1+ \cdots + a_{p, p-1}k_{p-1}))$.
- $b_i$, $c_i$ e $a_{ij}$: constantes obtidas igualando-se a fórmula geral de Runge-Kutta com os termos da expansão em série de Taylor de mesma ordem.
- $k_i$: relações de recorrência (cálculo computacional eficiente).
Uma demonstração completa do método de Runge-Kutta pode ser encontrada em livros como a referência bibliográfica [2]. No que segue, limitar-nos-emos a apresentar as fórmulas necessárias.
1.2 - Métodos de Runge-Kutta de $2^a$ Ordem
O método de Runge-Kutta de $2^a$ ordem concorda com a precisão do método de série de Taylor até os termos de $2^a$ ordem em h: $$y_{i+1}=y_i+hf(x_i, y_i) + \frac{h^2}{2}\left[\frac{\partial f(x_i, y_i)}{\partial x} + f(x_i, y_i)\frac{\partial f(x_i, y_i)}{\partial y} \right]$$
Usando a notação simplificada, $f_i=f(x_i, y_i)$, temos:
\begin{equation}
y_{i+1}=y_i+hf_i + \frac{h^2}{2}\left[\frac{\partial f_i}{\partial x} + f_i \frac{\partial f_i}{\partial y} \right]
\end{equation}
Considerando, agora, a definição do método de Runge-Kutta de $2^a$ ordem:
\begin{equation}
y_{i+1}=y_i+h(b_{1}f(x_i, y_i) + b_{2}f(x_{i}+c_{2}h, y_{i}+ha_{21}k_1)
\end{equation}
Expandindo $f(x, y)$, em série de Taylor, em torno de $(x_i, y_i)$ (retendo somente os termos de derivada primeira), temos:
$$f(x_{i}+c_{2}h, y_{i}+ha_{21}k_1) \approx f_i + c_{2}h \frac{\partial f_i}{\partial x}+a_{21}h f_i \frac{\partial f_i}{\partial y}$$
Substituindo esse resultado na equação anterior, e rearranjando, teremos:
\begin{equation}
y_{i+1}=y_i+h(b_1 + b_2)f_i + h^2 \left(b_{2}c_{2}\frac{\partial f_i}{\partial x} + b_{2}a_{21}f_i \frac{\partial f_i}{\partial y} \right)
\end{equation}
Assim, para haver concordância com o método de série de Taylor, resultado (4), é preciso que: $$b_1+b_2 = 1 \ \ \ \mbox{e} \ \ \ b_{2}c_{2}=\frac{1}{2} \ \ \ \mbox{e} \ \ \ b_{2}a_{21}=\frac{1}{2}.$$
- Resultado: Sistema não linear com 3 equações e 4 incógnitas, o que corresponde a uma variedade de métodos de segunda ordem.
1.2.1 - Métodos de Euler Modificado ($b_2=1$, $b_1=0$, $c_2=a_{21}=1/2$)
Dado um P.V.I, $y' = f(x, y)$, $y(x_0)=x_0$. A implementação deste método é dada pelas expressões:
- $y_{i+1} = y_i + h.k_2$
- $k_1 = f(x_i, y_i)$
- $k_2 = f(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2}k_{1})$
- com $x_{i+1} = x_i + h$, para $h>0$ próximo de $0$, $i=0, 1, 2, \cdots $ .
Para cada valor inteiro de $i$, a partir de $i=0$, calculam-se: $$x_{i+1} \ \ \rightarrow \ \ k_1 \ \ \rightarrow \ \ k_2 \ \ \rightarrow \ \ y_{i+1}$$
Repete-se essa sequência de cálculos recursivamente, até chegar no valor de $y_i$ desejado.
1.2.2 - Métodos de Euler Melhorado ou de Heun ($b_2=1/2$, $b_1=1/2$, $c_2=a_{21}=1$)
Dado um P.V.I, $y' = f(x, y)$, $y(x_0)=x_0$. A implementação deste método é dada pelas expressões:
- $y_{i+1} = y_i + \frac{h}{2}\left(k_1 + k_2 \right)$
- $k_1 = f(x_i, y_i)$
- $k_2 = f(x_{i}+h, y_{i}+hk_{1})$
- com $x_{i+1} = x_i + h$, para $h>0$ próximo de $0$, $i=0, 1, 2, \cdots $ .
Para cada valor inteiro de $i$, a partir de $i=0$, calculam-se: $$x_{i+1} \ \ \rightarrow \ \ k_1 \ \ \rightarrow \ \ k_2 \ \ \rightarrow \ \ y_{i+1}$$
Repete-se essa sequência de cálculos recursivamente, até chegar no valor de $y_i$ desejado.
1.3 - Métodos de Runge-Kutta de Ordem Superiores
De modo semelhante, podem ser deduzidas as fórmulas de Runge-Kutta de ordens superiores.
Em cada ordem, também haverá uma infinidade de versões. A seguir serão fornecidas apenas as fórmulas mais conhecidas para os métodos de Runge-Kutta de $3^a$ e $4^a$ ordens:
1.3.1 - Métodos Runge-Kutta de $3^a$ Ordem
Dado um P.V.I, $y' = f(x, y)$, $y(x_0)=x_0$. A implementação deste método é dada pelas expressões:
- $y_{i+1} = y_i + \frac{h}{6}\left(k_1 + 4k_2 + k_3 \right)$
- $k_1 = f(x_i, y_i)$
- $k_2 = f(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2}k_{1})$
- $k_3 = f(x_{i}+h, y_{i} - hk_{1} + 2hk_{2})$
- com $x_{i+1} = x_i + h$, para $h>0$ próximo de $0$, $i=0, 1, 2, \cdots $.
Para cada valor inteiro de $i$, a partir de $i=0$, calculam-se: $$x_{i+1} \ \ \rightarrow \ \ k_1 \ \ \rightarrow \ \ k_2 \ \ \rightarrow \ \ k_3 \ \ \rightarrow \ \ y_{i+1}$$
Repete-se essa sequência de cálculos recursivamente, até chegar no valor de $y_i$ desejado.
1.3.2 - Métodos Runge-Kutta de $4^a$ Ordem
Dado um P.V.I, $y' = f(x, y)$, $y(x_0)=x_0$. A implementação deste método é dada pelas expressões:
- $y_{i+1} = y_i + \frac{h}{6}\left(k_1 + 2k_2 + 2k_3 + k_4 \right)$
- $k_1 = f(x_i, y_i)$
- $k_2 = f(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2}k_{1})$
- $k_3 = f(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2}k_{2})$
- $k_4 = f(x_{i}+h, y_{i} + hk_{3})$
- com $x_{i+1} = x_i + h$, para $h>0$ próximo de $0$, $i=0, 1, 2, \cdots $.
Para cada valor inteiro de $i$, a partir de $i=0$, calculam-se: $$x_{i+1} \ \ \rightarrow \ \ k_1 \ \ \rightarrow \ \ k_2 \ \ \rightarrow \ \ k_3 \ \ \rightarrow \ \ k_4 \ \ \rightarrow \ \ y_{i+1}$$
Repete-se essa sequência de cálculos recursivamente, até chegar no valor de $y_i$ desejado.
Nota: O método de Runge-Kutta de $4^a$ ordem é o mais usado na solução numérica de problemas com equações diferenciais ordinárias.
1.4 - Exemplo usando o Método de Runge-Kutta de $2^a$ e $4^a$ Ordem
A equação diferencial ordinária de $1^{a}$ ordem escolhida será (Boyce, W. E., Diprima, R. C. Equações Diferenciais Elementares e Problemas de Valor de Contorno. Ed. 7, pp. 420):
\begin{equation}
\left\{
\begin{array}{ll}
\frac{dy}{dx}=1-x+4.y\\
y(0)=1
\end{array}
\right.
\end{equation}
Esta equação será resolvida de $x=0$ a $x=2$. A solução da equação diferencial (7) com a condição inicial (P.V.I.) é conhecida:
\begin{equation}
y(x)=\frac{1}{4}.x-\frac{3}{16}+\frac{19}{16}e^{4.x}
\end{equation}
A solução numérica é encontrada com a avaliação das equações do Método de Euler (Runge-Kutta de $1^a$ ordem), Euler modificado (Runge-Kutta de $2^a$ ordem) e do Método de Runge-Kutta de $4^a$ ordem, apresentadas acima, com a condição inicial, $x_0=0$ e $y_0=1$.
Para efeitos de comparação, usaremos dois valores para o passo h=0.1 (Figura 2) e h=0.01 (Figura 3), juntamente com a solução algébrica (8).
1.4.1 - Resultados obtidos pelos Métodos de Euler, Euler modificado e de Runge-Kutta de $4^a$ ordem
 |
| Figura 2: Métodos de Runge-Kutta com passo de integração $h=0.1$. |
 |
| Figura 3: Métodos de Runge-Kutta com passo de integração $h=0.01$. |
Por torna-se um processo demasiadamente repetitivo pelo número de iterações, é comum utilizar o método com o auxílio de uma linguagem de programação.
1.5 - Métodos de Runge-Kutta implementado em linguagem de programação.
Um programa escrito em C/C++ é apresentado a seguir. Uma parte do código-fonte pode ser retirada sem problemas, pois trata-se de rotinas voltadas para mostrar a interatividade entre o aplicativo gnuplot (para plotar gráficos) e a linguagem programação C/C++. Os dados obtidos são impressos em um arquivo de nome "runge_kutta.txt", podendo ser plotado usando o Origin, qtiplot, MatLab, SciLab, dentre outros.
/*=================== */
/* Métodos de Runge-Kutta */
/*=================== */
#include <stdio.h>
#include <stdlib.h>
#include <cmath>
FILE *fp;
static char nome[]="runge_kutta.txt";
void scrip_gnuplot(char str[25])
{
fp=fopen("rk_2_4.plt", "w");
fprintf(fp, "reset\n");
fprintf(fp, "set title \"Metodos de Runge Kutta\" \n");
fprintf(fp, "set xlabel \"Xn\" \n");
fprintf(fp, "set ylabel \"Yn\" \n");
fprintf(fp, "set key left \n");
fprintf(fp, "set term jpeg \n" );
fprintf(fp, "set output \"RK_2_4.jpeg\" \n");
fprintf(fp, "plot \'%s\' u 1:2 t \" Euler \" w lp ls 7 lc 1 lw 1, \'%s\' u 1:3 t \" Euler Modificado \" w lp ls 7 lc 2 lw 1\n", str, str);
fprintf(fp, "replot \'%s\' u 1:4 t \" Runge-Kutta 4a ordem \" w lp ls 7 lc 3 lw 1, \'%s\' u 1:5 t \" Analitica \" w l lc -1\n", str, str);
fprintf(fp, "set output; set term wxt \n");
fprintf(fp, "replot \n");
fprintf(fp, "pause -1 \"Continuar?\" ");
fclose(fp);
}
// Definição da equação diferencial: dy/dx=f(x,y)
double f(double x, double y)
{
return (1-x+4*y);
}
// Definiçao da solução analitica da equação diferencial
double y(double x)
{
return ((1.0/4.0)*x - (3.0/16.0) + (19.0/16.0)*exp(4.0*x));
}
// Definiçao do método de euler
double euler(double x, double y, double h)
{
double k1;
k1 = f(x,y);
y = y + h*k1;
return y;
}
// Definiçao do método de euler modificado
double euler_modificado(double x, double y, double h)
{
double k1, k2;
k1 = f(x,y);
k2 = f(x+0.5*h, y+0.5*h*k1);
y = y + h*k2;
return y;
}
// Definiçao do método de runge-kutta de 4a ordem
double runge_kutta_4(double x, double y, double h)
{
double k1, k2, k3, k4;
k1 = f(x,y);
k2 = f(x+0.5*h, y+0.5*h*k1);
k3 = f(x+0.5*h, y+0.5*h*k2);
k4 = f(x+h, y+h*k3);
y = y + h*(k1+2*k2+2*k3+k4)/6.0;
return y;
}
int main(void)
{
double x0, y0, xmax, h; // variaveis de entrada
double xn, yn_e, yn_em, yn_rk4;
double y_e, y_em, y_rk4;
// Dados de entrada:
x0=0.0;
xmax=2.0;
y0=1.0;
h=0.01;
// -----------------
fp=fopen(nome,"w");
xn=x0;
yn_e=y0;
yn_em=y0;
yn_rk4=y0;
while (xn<xmax)
{
fprintf(fp, "%f \t %f \t %f \t %f \t %f\n", xn, yn_e, yn_em, yn_rk4, y(xn));
y_e = euler(xn, yn_e, h);
y_em =euler_modificado(xn, yn_em, h);
y_rk4=runge_kutta_4(xn, yn_rk4, h);
xn=xn+h;
yn_e = y_e;
yn_em =y_em;
yn_rk4=y_rk4;
}
fclose(fp);
scrip_gnuplot(nome);
system("gnuplot rk_2_4.plt");
return 0;
}
1.6 - Conclusão
A resolução numérica pode ter grau crescente de aproximação, de acordo com o método numérico escolhido e da escolha do valor do passo de integração. Para os valores do passo de integração analisados, observamos que o método de Euler não se mostra uma boa escolha, pois seus resultados não são nada precisos, quando comparado aos dois outros métodos. Já no primeiro caso, obtivemos uma
boa aproximação por parte do método de Runge-Kutta de $4^a$ ordem. E, no segundo caso, já se verifica uma coincidência entre os métodos de Euler modificado e de Runge-Kutta de $4^a$ ordem com solução exata conhecida até onde se observou com passo de integração
$h=0.01$, ou seja, o "erro" ou diferença entre a aproximação e a
solução exata é praticamente nula para todos os pontos.
Assim,
diante dos exemplos estudados, concluímos que o Método de Runge-Kutta de $4^a$ ordem é bastante eficaz para resolução de EDOs de primeira ordem, o que explica o porquê de ser o método de passo simples mais utilizado por engenheiros e cientistas na resolução numérica de equações diferenciais ordinárias.
1.7 - Referências
[1]
W. E. Boyce, C. R. Diprima, "Equações Diferenciais Elementares e
Problemas de Valor de Contorno", LTC, Rio de Janeiro, 2011.
[2] M. A. G. Ruggiero, V. L. R. Lopes, "Cálculo Numérico: Aspectos Teóricos Computacionais", Makron Books, São Paulo, 1996.
[3]
G. Baratto, "Solução de Equações Diferenciais Ordinárias Usando Métodos
Numéricos", Departamento de Eletrônica e Computação - Estudo de Casos em
Engenharia Elétrica - UFSM, 2007.
[4] L. N. de Andrade, "Cálculo Numérico: Introdução à Matemática Computacional", Departamento de Matemática - UFPB, 2013.
[4] L. N. de Andrade, "Cálculo Numérico: Introdução à Matemática Computacional", Departamento de Matemática - UFPB, 2013.
Nesta postagem, o nosso objetivo, além de apresentar este importante tema da Matemática, é o de fornecer exemplos da interatividade entre as linguagem de programação C/C++ e o aplicativo gnuplot, que juntos minimizam as tarefas de uma pesquisa.
sábado, 18 de abril de 2015
Solução Numérica de Equações Diferenciais Ordinárias usando o Método de Euler
1.0 INTRODUÇÃO
onde $y_0$ é um número dado. Os problemas de valor inicial (P.V.I) de ordem superior podem ser reduzidos a sistemas de primeira ordem através de variáveis auxiliares, o que permite a utilização do método numérico aqui apresentado.
Para resolver numericamente uma E.D.O. com P.V.I. (equação 1), supõem-se que ela satisfaz às condições de existência e unicidade. Esta solução numérica será encontrada para um conjunto finito de pontos (um intervalo fechado $[a,b]$) no eixo das abscissas.
Tomando-se $m$ subintervalos deste intervalo $[a, b]$, sendo $m \geq 1$, é possível determinar $m+1$ pontos onde as soluções numéricas devem ser calculados. Estes pontos $x_j \in [a, b]$ são igualmente espaçados entre si por um fator $h$, onde $x_j=x_0+j.h$, sendo que $x_0=a, \ \ x_m=b, \ \ h=(b-a)/m \ \ \mbox{e} \ \ j=0, 1, 2, \cdots, m$. O conjunto $\left\{x_0, x_1, x_2, \cdots, x_m \right\}$ obtido denomina-se rede ou malha de $[a, b]$.
Para facilitar a interpretação dos métodos, convenciona-se a seguinte notação:
1.1 - MÉTODO DE EULER
O método de Euler, também conhecido como método da reta tangente, é um dos métodos mais antigos que se conhece para solução de equações diferenciais ordinárias. O método é muito atraente por sua simplicidade, mas não muito usado em problemas práticos, dentre muitos outros métodos, pois apesar de simples, para conseguir "boas" aproximações é necessário um número maior de cálculos.
1.1.1 - Derivação da Fórmula de Euler
Seja uma E.D.O. com P.V.I. dada pela equação 1. O que se deseja é encontrar as aproximações $y_1, y_2, \cdots, y_m$ para as soluções exatas $y(x_1), y(x_2), \cdots, y(x_m)$.
Sendo que o ponto inicial $(x_0, y_0)$ é fornecido pelo problema, o primeiro passo então é a busca de $y_1$. Para isto, aproximando-se a solução $y(x)$ por uma Série de Taylor no ponto $x=x_0$ e truncando no segundo termo, tem-se:
\begin{equation}
y(x)=y(x_0)+y'(x_0).(x-x_0)
\end{equation}
Para $x=x_1$ tem-se:
\begin{equation}
y(x_1)=y(x_0)+(x_1-x_0).y'(x_0)
\end{equation}
Lembrando que, como os valores exatos $y(x_n)$ são desconhecidos, são utilizados os valores aproximados $y_n$ e que $x_1-x_0=h$ e $y'(x_0)=f(x_0,y_0)$, onde $h$ é a distância entre os pontos consecutivos $x_n$ e $x_{n+1}$, então:
\begin{equation}
y_1=y_0+h.f(x_0, y_0)
\end{equation} Para encontrar $y_2$ na abscissa $x=x_2$ adota-se o mesmo procedimento (tomando-se ($x_1, y_1$) como ponto de partida). Assim, a solução aproximada é:
\begin{equation}
y_2=y_1+h.f(x_1, y_1)
\end{equation}
Assim a solução numérica fornecida pelo método de Euler é a poligonal com vértices $(x_0, y_0), (x_1, y_1), (x_2, y_2), \cdots, (x_{n+1}, y_{n+1})$, onde os segmentos de reta no intervalo $(x_k, x_{k+1})$, $k=0, 1, 2, \cdots, n$ têm como equação $L_k(x)=y_k+f(x_k,y_k)(x-x_k)$.
Nesta postagem, o nosso objetivo, além de apresentar este importante tema da Matemática, é o de fornecer exemplos da interatividade entre as linguagem de programação C/C++ e o aplicativo gnuplot, que juntos minimizam as tarefas de uma pesquisa.
Uma
Equação Diferencial é uma equação que envolve derivadas
de uma ou mais funções. Elas servem para descrever o comportamento
de sistemas dinâmicos e possuem enorme aplicação em diversas
áreas, como em engenharia (no estudo do comportamento de um circuito
elétrico ou do movimento oscilatório de estruturas), Física
(lançamento de foquetes, oscilações forçadas, ...), Biologia
(crescimento de populações de bactérias) ou economia (aplicações
financeiras). Elas são classificadas de acordo com o seu tipo,
ordem e grau. Se uma equação diferencial envolve derivadas de uma
função de uma única variável independente, ela é dita ser
Equação Diferencial Ordinária. Caso
a equação diferencial envolva as derivadas parciais de uma função
de duas ou mais variáveis independentes, é uma Equação
Diferencial Parcial.
Uma equação diferencial ordinária (ou E.D.O.) de ordem n pode ser expressa na seguinte forma:
$$\frac{d^n\,y}{dx^n}=F \left(x, y,\frac{dy}{dx}, \frac{d^{2}y}{dx^{2}}, \cdots, \frac{d^{n-1}y}{dx^{n-1}} \right)$$
onde $x$ é a variável independente, $y$ é uma função desta variável independente e $\frac{d^k\,y}{dx^k}$, com $k=1,2,3, \cdots, n$ são as derivadas de $y$ em relação a $x$.
Há vários métodos que resolvem analiticamente uma E.D.O., entretanto nem sempre é possível obter uma solução analítica. Neste caso, os métodos numéricos são uma saída para se encontrar uma solução aproximada.
Nesta postagem, vamos nos concentrar em problemas de valor inicial (P.V.I.) em sua forma mais simples que são as equações diferenciais ordinárias de primeira ordem:
\begin{equation}
\left\{
\begin{array}{ll}
\frac{dy}{dx}=f(x,y)\\
y(x_0)=y_0
\end{array}
\right.
\end{equation}
Uma equação diferencial ordinária (ou E.D.O.) de ordem n pode ser expressa na seguinte forma:
$$\frac{d^n\,y}{dx^n}=F \left(x, y,\frac{dy}{dx}, \frac{d^{2}y}{dx^{2}}, \cdots, \frac{d^{n-1}y}{dx^{n-1}} \right)$$
onde $x$ é a variável independente, $y$ é uma função desta variável independente e $\frac{d^k\,y}{dx^k}$, com $k=1,2,3, \cdots, n$ são as derivadas de $y$ em relação a $x$.
Há vários métodos que resolvem analiticamente uma E.D.O., entretanto nem sempre é possível obter uma solução analítica. Neste caso, os métodos numéricos são uma saída para se encontrar uma solução aproximada.
Nesta postagem, vamos nos concentrar em problemas de valor inicial (P.V.I.) em sua forma mais simples que são as equações diferenciais ordinárias de primeira ordem:
\begin{equation}
\left\{
\begin{array}{ll}
\frac{dy}{dx}=f(x,y)\\
y(x_0)=y_0
\end{array}
\right.
\end{equation}
onde $y_0$ é um número dado. Os problemas de valor inicial (P.V.I) de ordem superior podem ser reduzidos a sistemas de primeira ordem através de variáveis auxiliares, o que permite a utilização do método numérico aqui apresentado.
Para resolver numericamente uma E.D.O. com P.V.I. (equação 1), supõem-se que ela satisfaz às condições de existência e unicidade. Esta solução numérica será encontrada para um conjunto finito de pontos (um intervalo fechado $[a,b]$) no eixo das abscissas.
Tomando-se $m$ subintervalos deste intervalo $[a, b]$, sendo $m \geq 1$, é possível determinar $m+1$ pontos onde as soluções numéricas devem ser calculados. Estes pontos $x_j \in [a, b]$ são igualmente espaçados entre si por um fator $h$, onde $x_j=x_0+j.h$, sendo que $x_0=a, \ \ x_m=b, \ \ h=(b-a)/m \ \ \mbox{e} \ \ j=0, 1, 2, \cdots, m$. O conjunto $\left\{x_0, x_1, x_2, \cdots, x_m \right\}$ obtido denomina-se rede ou malha de $[a, b]$.
Para facilitar a interpretação dos métodos, convenciona-se a seguinte notação:
- $y(x_j)$ é a solução exata do P.V.I., obtida analiticamente;
- $y_j$ é a solução numérica.
1.1 - MÉTODO DE EULER
O método de Euler, também conhecido como método da reta tangente, é um dos métodos mais antigos que se conhece para solução de equações diferenciais ordinárias. O método é muito atraente por sua simplicidade, mas não muito usado em problemas práticos, dentre muitos outros métodos, pois apesar de simples, para conseguir "boas" aproximações é necessário um número maior de cálculos.
1.1.1 - Derivação da Fórmula de Euler
Seja uma E.D.O. com P.V.I. dada pela equação 1. O que se deseja é encontrar as aproximações $y_1, y_2, \cdots, y_m$ para as soluções exatas $y(x_1), y(x_2), \cdots, y(x_m)$.
Sendo que o ponto inicial $(x_0, y_0)$ é fornecido pelo problema, o primeiro passo então é a busca de $y_1$. Para isto, aproximando-se a solução $y(x)$ por uma Série de Taylor no ponto $x=x_0$ e truncando no segundo termo, tem-se:
\begin{equation}
y(x)=y(x_0)+y'(x_0).(x-x_0)
\end{equation}
Para $x=x_1$ tem-se:
\begin{equation}
y(x_1)=y(x_0)+(x_1-x_0).y'(x_0)
\end{equation}
Lembrando que, como os valores exatos $y(x_n)$ são desconhecidos, são utilizados os valores aproximados $y_n$ e que $x_1-x_0=h$ e $y'(x_0)=f(x_0,y_0)$, onde $h$ é a distância entre os pontos consecutivos $x_n$ e $x_{n+1}$, então:
\begin{equation}
y_1=y_0+h.f(x_0, y_0)
\end{equation} Para encontrar $y_2$ na abscissa $x=x_2$ adota-se o mesmo procedimento (tomando-se ($x_1, y_1$) como ponto de partida). Assim, a solução aproximada é:
\begin{equation}
y_2=y_1+h.f(x_1, y_1)
\end{equation}
Se utilizarmos esse processo recursivas vezes chegaremos a uma fórmula geral, e esse procedimento é chamado método de Euler:
\begin{equation}
y_{n+1}=y_n+h.f(x_n, y_n)
\end{equation}
\begin{equation}
y_{n+1}=y_n+h.f(x_n, y_n)
\end{equation}
onde $x_n=x_{n-1}+h=x_0+n.h$, com $n=0, 1, 2, \cdots, m-1$.
Assim a solução numérica fornecida pelo método de Euler é a poligonal com vértices $(x_0, y_0), (x_1, y_1), (x_2, y_2), \cdots, (x_{n+1}, y_{n+1})$, onde os segmentos de reta no intervalo $(x_k, x_{k+1})$, $k=0, 1, 2, \cdots, n$ têm como equação $L_k(x)=y_k+f(x_k,y_k)(x-x_k)$.
Na figura 1, ilustramos a idéia do método de Euler. Veja que quanto menor o valor da diferença entre $x_{n+1}$ e $x_n$ menor o erro da estimativa para $y_{n+1}$.
1.1.2 - Exemplo usando o Método de Euler
A equação diferencial ordinária de $1^{a}$ ordem escolhida será (Boyce, W. E., Diprima, R. C. Equações Diferenciais Elementares e Problemas de Valor de Contorno. Ed. 7, pp. 420):
\begin{equation}
\left\{
\begin{array}{ll}
\frac{dy}{dx}=1-x+4.y\\
y(0)=1
\end{array}
\right.
\end{equation}
Esta equação será resolvida de $x=0$ a $x=2$. A solução da equação diferencial (7) com a condição inicial (P.V.I.) é conhecida:
\begin{equation}
y(x)=\frac{1}{4}.x-\frac{3}{16}+\frac{19}{16}e^{4.x}
\end{equation}
A solução numérica é encontrada com a avaliação das equações (6):
\begin{equation}
x_{n+1}=x_n+h
\end{equation}
| Figura 1: Ilustração do método de Euler |
A equação diferencial ordinária de $1^{a}$ ordem escolhida será (Boyce, W. E., Diprima, R. C. Equações Diferenciais Elementares e Problemas de Valor de Contorno. Ed. 7, pp. 420):
\begin{equation}
\left\{
\begin{array}{ll}
\frac{dy}{dx}=1-x+4.y\\
y(0)=1
\end{array}
\right.
\end{equation}
Esta equação será resolvida de $x=0$ a $x=2$. A solução da equação diferencial (7) com a condição inicial (P.V.I.) é conhecida:
\begin{equation}
y(x)=\frac{1}{4}.x-\frac{3}{16}+\frac{19}{16}e^{4.x}
\end{equation}
A solução numérica é encontrada com a avaliação das equações (6):
\begin{equation}
x_{n+1}=x_n+h
\end{equation}
e
\begin{equation}
y_{n+1}=y_n+h.f(x_n, y_n)=y_n+h.(1-x_n+4.y_n)
\end{equation}
Com a condição inicial, $x_0=0$ e $y_0=1$, os próximos valores são calculados com o uso recursivo das equações (9) e (10). Para efeitos de comparação, usaremos dois valores para o passo h=0.01 (Figura 2) e h=0.001 (Figura 3), juntamente com a solução algébrica (8).
1.1.3 - Resultados
Por torna-se um processo demasiadamente repetitivo pelo número de iterações, é comum utilizar o método com o auxílio de uma linguagem de programação.
1.2 - Método de Euler implementado em linguagem de programação.
Um programa escrito em C/C++ é apresentado a seguir. Uma parte do código-fonte pode ser retirada sem problemas, pois trata-se de rotinas voltadas para mostrar a interatividade entre o aplicativo gnuplot (para plotar gráficos) e a linguagem programação C/C++. Os dados obtidos são impressos em um arquivo de nome "metodo_euler.txt", podendo ser plotado usando o Origin, qtiplot, MatLab, SciLab, dentre outros.
/*==========================*/
\begin{equation}
y_{n+1}=y_n+h.f(x_n, y_n)=y_n+h.(1-x_n+4.y_n)
\end{equation}
Com a condição inicial, $x_0=0$ e $y_0=1$, os próximos valores são calculados com o uso recursivo das equações (9) e (10). Para efeitos de comparação, usaremos dois valores para o passo h=0.01 (Figura 2) e h=0.001 (Figura 3), juntamente com a solução algébrica (8).
1.1.3 - Resultados
 |
| Figura 2: Gráfico apresentando a solução numérica com h=0.01 (método de Euler) e análitica (eq. 8) |
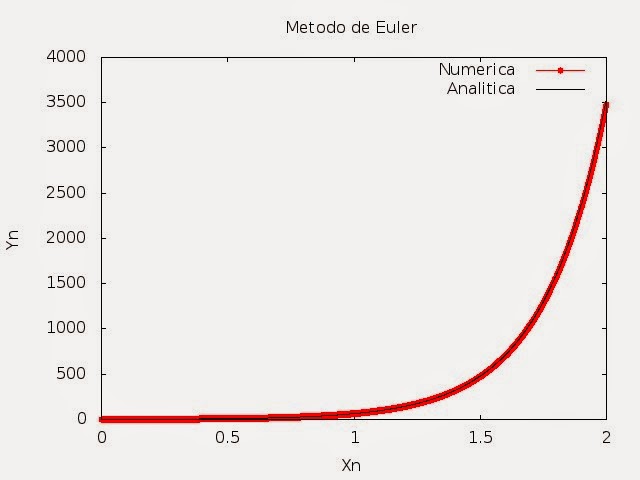 |
| Figura 3: Gráfico apresentando a solução numérica com h=0.001 (método de Euler) e análitica (eq. 8) |
1.2 - Método de Euler implementado em linguagem de programação.
Um programa escrito em C/C++ é apresentado a seguir. Uma parte do código-fonte pode ser retirada sem problemas, pois trata-se de rotinas voltadas para mostrar a interatividade entre o aplicativo gnuplot (para plotar gráficos) e a linguagem programação C/C++. Os dados obtidos são impressos em um arquivo de nome "metodo_euler.txt", podendo ser plotado usando o Origin, qtiplot, MatLab, SciLab, dentre outros.
/*==========================*/
/* Método de Euler */
/*==========================*/
#include <stdio.h>
#include <stdlib.h>
#include <cmath>
FILE *fp;
static char nome[]="metodo_euler.txt";
// Função para plotar o gráfico via o aplicativo gnuplot (opcional no programa)
void scrip_gnuplot(char str[25])
{
fp=fopen("metodo_euler.plt", "w");
fprintf(fp, "reset\n");
fprintf(fp, "set title \"Metodo de Euler\" \n");
fprintf(fp, "set xlabel \"Xn\" \n");
fprintf(fp, "set ylabel \"Yn\" \n");
fprintf(fp, "set term jpeg \n" );
fprintf(fp, "set output \"Metodo_Euler.jpg\" \n");
fprintf(fp, "plot \'%s\' u 1:2 t \" Numerica \" w lp ls 7 lc 1 lw 1, \'%s\' u 1:3 t \" Analitica \" w l lc -1\n", str, str);
fprintf(fp, "set output; set term wxt \n");
fprintf(fp, "replot \n");
fprintf(fp, "pause -1 \"Continuar?\" ");
fclose(fp);
}
// Definição da equação diferencial: dy/dx=f(x,y)
double f(double x, double y)
{
return (1-x+4*y);
}
// Definiçao da solução analitica da equação diferencial
double y(double x)
{
return ((1.0/4.0)*x - (3.0/16.0) + (19.0/16.0)*exp(4.0*x));
}
int main(void)
{
double x0, y0, xmax, h; // variaveis de entrada
double xn, yn, xn1, yn1;
// Dados de entrada:
x0=0.0;
xmax=2.0;
y0=1.0;
h=0.001; // passo h
// -----------------
fp=fopen(nome,"w");
xn=x0;
yn=y0;
while (xn<xmax)
{
fprintf(fp, "%f \t %f \t %f\n", xn, yn, y(xn));
yn1=yn+h*f(xn,yn);
xn1=xn+h;
xn=xn1;
yn=yn1;
}
fclose(fp);
scrip_gnuplot(nome); // chamada opcional no programa
system("gnuplot metodo_euler.plt"); // chamada opcional no programa
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include <cmath>
FILE *fp;
static char nome[]="metodo_euler.txt";
// Função para plotar o gráfico via o aplicativo gnuplot (opcional no programa)
void scrip_gnuplot(char str[25])
{
fp=fopen("metodo_euler.plt", "w");
fprintf(fp, "reset\n");
fprintf(fp, "set title \"Metodo de Euler\" \n");
fprintf(fp, "set xlabel \"Xn\" \n");
fprintf(fp, "set ylabel \"Yn\" \n");
fprintf(fp, "set term jpeg \n" );
fprintf(fp, "set output \"Metodo_Euler.jpg\" \n");
fprintf(fp, "plot \'%s\' u 1:2 t \" Numerica \" w lp ls 7 lc 1 lw 1, \'%s\' u 1:3 t \" Analitica \" w l lc -1\n", str, str);
fprintf(fp, "set output; set term wxt \n");
fprintf(fp, "replot \n");
fprintf(fp, "pause -1 \"Continuar?\" ");
fclose(fp);
}
// Definição da equação diferencial: dy/dx=f(x,y)
double f(double x, double y)
{
return (1-x+4*y);
}
// Definiçao da solução analitica da equação diferencial
double y(double x)
{
return ((1.0/4.0)*x - (3.0/16.0) + (19.0/16.0)*exp(4.0*x));
}
int main(void)
{
double x0, y0, xmax, h; // variaveis de entrada
double xn, yn, xn1, yn1;
// Dados de entrada:
x0=0.0;
xmax=2.0;
y0=1.0;
h=0.001; // passo h
// -----------------
fp=fopen(nome,"w");
xn=x0;
yn=y0;
while (xn<xmax)
{
fprintf(fp, "%f \t %f \t %f\n", xn, yn, y(xn));
yn1=yn+h*f(xn,yn);
xn1=xn+h;
xn=xn1;
yn=yn1;
}
fclose(fp);
scrip_gnuplot(nome); // chamada opcional no programa
system("gnuplot metodo_euler.plt"); // chamada opcional no programa
return 0;
}
1.3 - Conclusão
Através do Método Numérico de Euler, obtemos uma boa aproximação para a solução $y(x)$ de uma E.D.O. de primeira ordem. No primeiro caso, obtivemos uma aproximação considerada "boa" em boa parte do intervalo considerado, $[0, 2]$. Já no segundo caso, obtivemos uma aproximação coincidente com a solução exata conhecida até onde se observou com passo de integração $h=0.001$, ou seja, o "erro" ou diferença entre a aproximação e a solução exata é praticamente nula para todos os pontos.
Assim, diante dos exemplos estudados, concluímos que o Método Numérico de Euler é eficaz para resolução de EDOs de primeira ordem, apresentando em alguns casos erros pequenos que podem ser melhores ajustados através da escolha do passo de integração.
1.4 - Referências
[1] W. E. Boyce, C. R. Diprima, "Equações Diferenciais Elementares e Problemas de Valor de Contorno", LTC, Rio de Janeiro, 2011.
[2] M. A. G. Ruggiero, V. L. R. Lopes, "Cálculo Numérico: Aspectos Teóricos Computacionais", Makron Books, São Paulo, 1996.
[3] G. Baratto, "Solução de Equações Diferenciais Ordinárias Usando Métodos Numéricos", Depto de Eletrônica e Computação - Estudo de Casos em Engenharia Elétrica, 2007.
Nesta postagem, o nosso objetivo, além de apresentar este importante tema da Matemática, é o de fornecer exemplos da interatividade entre as linguagem de programação C/C++ e o aplicativo gnuplot, que juntos minimizam as tarefas de uma pesquisa.
Assinar:
Postagens (Atom)